0
| 本文作者: sharpzero | 2017-03-23 17:07 |
雷锋网按:随着数据科学成为炙手可热的领域,相关的应聘岗位也多了起来。面试者们在准备应聘的过程中,往往会有一个疑问:面试官们会问些什么?我又应该如何回答? Gregory Piatetsky在KDnuggets上分享了17个紧跟热点的数据科学相关职位可能会接触的问题及答案。从AI未能正确预测2016年美国总统选举结果和第51届超级碗大逆转的经验教训,如何区分偏差和方差,预测变量数目越少越好,甚至到如何增强模型抵抗异常的鲁棒性都一应俱全,本文为第一部分,雷锋网做了相关编译。
去年,21个必知的数据科学相关职位面试问题和答案成为了年度浏览次数最多的帖子 ,页面浏览量超过了25万。 2017年,KDnuggets编辑为您带来超过17个新的和重要的数据科学相关职位面试问题和答案。本篇回答了下面六个问题:
运用数据科学知识未能正确预测2016美国总统选举(第51届超级碗大逆转)结果的教训
新的(不可见的)测试数据与训练数据分布的显著差异所导致的问题?
偏差和方差的定义以及它们与建模数据的关系是什么?
为什么更少个数的预测变量较佳?
二进制分类器性能评估采用何种错误指标衡量? 类不平衡的对策?超过2组的对策?
增加模型抗异常鲁棒性的方法?
Gregory Piatetsky的答案:
2016年11月8日大选之前,大多数选民认为希拉里·克林顿在大众选举和选举团选举分别占有大约3%的优势和70%到95%的获胜可能。 内特·希尔沃的FiveThirtyEight这样的大数据公司预测特朗普获胜的概率最高,约为30%,而纽约时报旗下的大数据公司的Upshot和普林斯顿选举联盟预测特朗普获胜的概率只有约15%,而像新闻博客网站赫芬顿邮报这样的民意调查媒体预测特朗普只有2%的胜率。 不过,特朗普赢了。 那么,数据科学家应该从中汲取哪些教训呢?

统计有效的预测需要满足两个条件:
1)足够多的历史数据
2)假设历史事件与我们需要预测结果的当前事件足够相似。
事件可以分为确定的(2 + 2总等于4)、强可预测(例如行星和卫星的轨道,掷硬币时头像一面落地的平均次数)、弱可预测(如选举和体育赛事)、随机(如公平的彩票)。
如果掷硬币1亿次,估计头像朝上的次数(平均)为5000万,标准差= 10,000(公式0.5 * SQRT(N)),可预测99.7%的头像朝上的次数将在平均值的3个标准偏差内。
但使用民意调查预测1亿人的投票要困难得多。调查者需要有代表性的样本,估计个体实际投票的可能性,做出许多合理和不合理的假设,避免有意或无意的偏见。
因为古老的选举团制度、各州(除缅因州和内布拉斯加州外)胜者全得、民调的需要以及预测结果各州独立导致总统选举结果的预测更为棘手。
下图显示,2016年美国总统选举民调结果在多个州与实际大相径庭,其中大多数低估了特朗普获得的选票,尤其在密歇根州,威斯康星州和宾夕法尼亚州这三个关键州,以上三州的选票都投给了特朗普。

资料来源: @ NateSilver538 推特,2016年11月9日。
有几个统计学家譬如Salil Mehta @salilstatistics认为民调不切实际,538的David Wasserman实际上在2016年9月的一篇《特朗普为何丢掉了大众选举却赢得了总统选举》阐述了上述观点,但大多数民调者错得离谱。
因此,数据科学家从中汲取的一条有价值的教训便是要质疑自己做出的假设 ,并且在对弱可预测事件进行预测时保持怀疑,尤其是针对基于人类行为的预测时更是如此。
其它重要的教训是:
检查数据质量 - 这次选举中民调没有覆盖所有选民
小心偏见:许多民调者可能是克林顿希拉里的支持者,不想质疑对其有利的结果。 例如,赫芬顿邮报预测克林顿希拉里有95%的获胜机会。
对2016年民调失败的其它分析可参考:
《特朗普获胜并非宣告大数据的死亡——它一直有缺陷》(连线)
《数据在预测选举失败中扮演了怎样的角色》(纽约时报)
《民调的重大挫败提供的六个数据科学可以汲取的教训》(Datanami)
《特朗普的选举:民调失败带给IT领域的数据技术方面的教训》(InformaitonWeek)
《为什么我要在美国有线电视新闻网直播吃虫子》(普林斯顿选举联盟的Sam Wang)
( 注意:该答案基于KDnuggets上的一篇旧帖子《选举预测失败于数据科学家的启示》)
还有另一个从统计学角度来看的小概率事件:2017年2月5日的第51届超级碗比赛中发生了剧情般的反转:半场结束后,亚特兰大猎鹰队21比3领先,第三节后比分扩大到了28比9。ESPN估计亚特兰大猎鹰当时胜券在握。
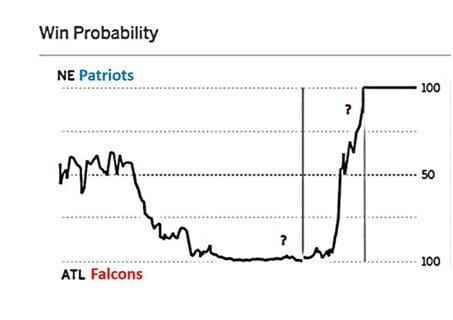
(参考:Salil Mehta tweet Salil Mehta tweet,2017年2月6日 )
从来没有一支队伍在这样的巨大比分优势下将冠军拱手相送。 然而,每场超级碗比赛都充满变数,这次可称得上是惊天逆转。 集超凡的技能(毕竟爱国者队决赛前也是夺冠热门)和运气(凭借 Julian Edelman好运的接球争取到了加时赛)于一身,爱国者队最终赢得比赛。
这次超级碗比赛也给了数据科学家另外一个有意义的教训。对弱可预测事件进行预测时,大多的自信是不可取的。在预测此类事件时需要了解风险因素,并尽量避免使用概率,或者如果必须使用数字,则需要具有宽泛的置信范围。
而如果呈现一边倒的预测,但它只是微弱的可预测事件,不妨坚持自己的观点——有时你甚至能击败赔率。
Gregory Piatetsky和Thuy Pham回答:
核心问题在于预测是错误的。
如果新测试数据在预测模型的关键参数与训练数据中非常不同,则说明预测模型不再有效。可能发生这一情况的主要原因在于样本选择偏差,种群漂移或非平稳环境。
这里的数据是静态的,但是训练实例是通过一种有偏差的方法获得的,例如数据到训练和测试的非均匀选择或非随机分割。
如果你有一个大的静态数据集,那么你应该随机分成训练/测试数据,测试数据的分布应该类似于训练数据。
这里的数据不是静态的,一部分人口用作训练数据,另一个部分用于测试。

(图via iwann )。
有时,训练数据和测试数据是通过不同的过程得到的 - 例如对一个群体测试的药物被给予可能具有显着差异的新群体。因此,基于训练数据的分类器性能较差。
一个提出的解决方案是应用统计测试来确定分类器使用的目标类和关键变量的概率是否显着不同,如果是,则使用新数据重新训练模型。
无论是由于时间或空间变化,培训环境与测试不同。
这与情况b类似,但适用于数据不是静态的情况——我们有一个数据流,我们定期对其进行抽样以开发未来行为的预测模型。 这发生在对抗分类问题中,例如垃圾邮件过滤和网络入侵检测,其中垃圾邮件发送者和黑客经常改变他们的行为。 另一个典型的案例是客户分析,其中客户行为随时间改变。 电话公司开发用于预测客户流失的模型或者信用卡公司开发预测交易欺诈的模型。 训练数据是历史数据,而(新的)测试数据是当前数据。
这种模型需要定期重新训练,并确定何时可以比较旧数据(训练集)和新数据中预测模型中关键变量的分布,如果有足够显着的差异,则该模型需要再培训。
有关更详细和技术的讨论,请参见下面的参考文献。
参考文献:
[1] Marco Saerens,Patrice Latinne,Christine Decaestecker:Adjusting the Outputs of a Classifier to New a Priori Probabilities:A Simple Procedure。 Neural Computation 14(1):21-41(2002)
[2]非固定环境中的机器学习:协变量适应的介绍,杉山杉山,Motoaki Kawanabe,MIT出版社,2012年,ISBN 0262017091,9780262017091
[3] Quora:《如果测试数据的分布明显不同于训练数据的分布,原因何在?》
[4] 《数据集转移的分类:方法和问题》 ,弗朗西斯科·赫雷拉,2011年。
[5] 《当训练和测试集不同:表征学习传递》,Amos Storkey,2013。
Matthew Mayo答案:
偏差是模型的预测与正确性的差距,而方差是这些预测在模型迭代之间变化的程度。
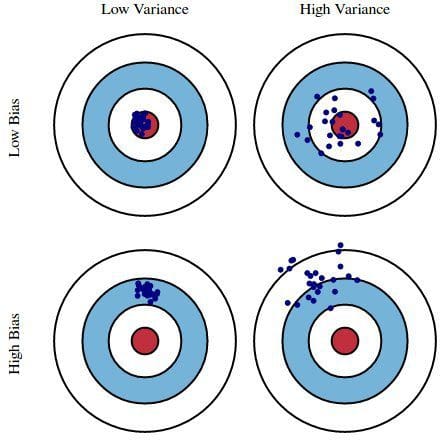
例如 ,以一个总统选举调查作为例子,我们可以通过偏差和方差的双重透镜解释调查中的错误:从电话簿中选择调查参与者会导致偏差;小样本量会导致方差。
最小化总模型误差依赖于偏差和方差误差的平衡。 理想情况下,模型是低方差的无偏差数据的集合的结果。 然而不幸的是,模型变得越复杂,它的趋势是偏差越小,但方差越大; 因此,最优模型需要考虑这两个属性之间的平衡。
交叉验证的统计评估方法在证明这种平衡的重要性,而找到这个平衡点也同样重要。 使用的数据折叠数量 - k倍交叉验证中的k值是一个重要的决定;值越低,误差估计中的偏差越大,方差越小。
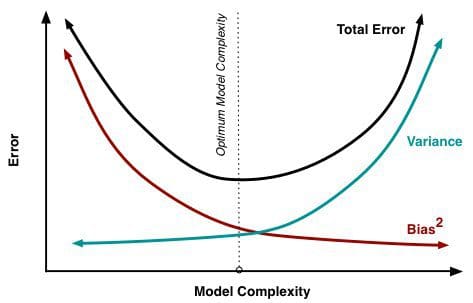
偏差和方差造成总误差 , 图像源
相反,当k被设置为等于实例数时,误差估计在偏差方面非常低,但具有高方差的可能性。
最重要的是,在建立模型时,偏差和方差是一个重要权衡的两个方面,即使是最常规的统计评价方法也直接依赖于这种权衡。
Anmol Rajpurohit的答案:
这里有几个原因,它可能是一个更好的主意,有更少的预测变量,而不是有很多:
如果你处理许多预测变量,那么在其中一些变量之间存在隐藏关系的可能性很高,从而导致冗余。 除非在数据分析的早期阶段识别和处理此冗余(通过仅选择非冗余预测变量),否则可能会对后续步骤造成巨大阻力。
也有可能不是所有的预测变量都对因变量具有相当大的影响。 您应该确保选择工作的预测变量集不具有任何不相关的变量 - 即使您知道数据模型将通过给予它们更低的重要性来处理它们。
注意:冗余和不相关是两个不同的概念 - 由于存在其他相关特征,相关特征可以是冗余的。
即使有大量的预测变量在其中任何一个之间没有关系,仍然优选使用较少的预测变量。 具有大量预测器(也称为复杂模型)的数据模型经常遭受过拟合的问题,在这种情况下,数据模型在训练数据上执行良好,但对测试数据执行得不好。
假设您有一个项目,其中有大量的预测变量,而且所有变量都是相关的(即对因变量有可测量的影响)。 所以,你显然想要与所有这些工作,以便有一个非常高的成功率的数据模型。 虽然这种方法听起来非常诱人,但实际考虑(如可用数据量,存储和计算资源,完成时间等)几乎不可能。
因此,即使您有大量相关的预测变量,使用较少的预测变量(通过特征选择或通过特征提取开发)是一个好主意。 这基本上类似于帕累托原理,其中指出,对于许多事件,大约80%的效果来自20%的原因。
关注这20%最重要的预测变量将有助于在合理的时间内建立具有相当成功率的数据模型,而不需要非实际数据量或其他资源。
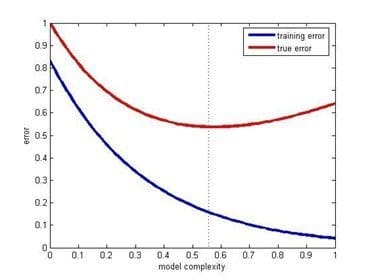
培训错误和测试错误vs模型复杂性(来源:发布在Quora由Sergul Aydore )
具有较少预测变量的模型更容易理解和解释。 由于数据科学步骤将由人类执行,并且结果将由人类呈现(并且希望被使用),因此考虑人类大脑的综合能力是重要的。 这基本上是一种折衷 - 你允许你的数据模型的成功率的一些潜在的好处,同时使你的数据模型更容易理解和优化。
这个因素是特别重要的,如果在你的项目结束时,你需要向一个人,谁不仅有兴趣不仅高成功率,而且在理解“发生”下发生的结果。
Prasad Pore 答案:
二进制分类涉及基于诸如性别,年龄,位置等独立变量将数据分为两组,例如客户是否购买特定产品(是/否)。
由于目标变量不连续,二进制分类模型预测目标变量的概率为Yes / No。 为了评估这样的模型,使用称为混淆矩阵的度量,也称为分类或相关矩阵。 在混淆矩阵的帮助下,我们可以计算重要的性能度量有:
真正速率(TPR)或命中率或召回或灵敏度= TP /(TP + FN)
假阳性率(FPR)或假警报率= 1 - 特异性= 1 - (TN /(TN + FP))
精度=(TP + TN)/(TP + TN + FP + FN)
错误率= 1-精度或(FP + FN)/(TP + TN + FP + FN)
精度= TP /(TP + FP)
F测量:2 /((1 /精确)+(1 /召回))
ROC(接收机工作特性)= FPR与TPR的关系曲线
AUC(曲线下面积)
Kappa统计
您可以在这里找到有关这些度量的更多详细信息: 测量分类模型精度的最佳指标 。
所有这些措施都应该与领域技能相平衡,例如,虽然更高的TPR表示对方不患癌的概率较大,但它对诊断癌症没有帮助。
在相同的癌症诊断数据的例子中,如果仅2%或更少的患者具有癌症,则这将出现类不平衡的情况,因为癌症患者的百分比与其他人群相比非常小。 有两个主要的方法来处理这个问题:
1. 成本函数的使用:在这种方法中,与成本矩阵(类似于混淆矩阵,但更关心假阳性和假阴性)的帮助来评估与错误分类数据相关联的成本。 主要目的是减少错误分类的成本。 假阴性的成本总是大于假阳性的成本。 例如错误地预测癌症患者是无癌症的,比错误地预测无癌症患者患有癌症更危险。
总成本= FN的成本* FN的计数+ FP的成本* FP的计数
2. 使用不同的采样方法 :在此方法中,可以使用过采样,欠采样或混合采样。 在过抽样中,少数种类观察被复制以平衡数据。 复制观察导致过度拟合,导致训练中的良好准确性,但不可见数据的准确性较低。在欠采样中,大多数类观察被移除导致信息的丢失。 它有助于减少处理时间和存储,但仅在具有大数据集时有用。
如果目标变量中有多个类,则形成尺寸等于类数量的混淆矩阵,并且可以为每个类计算所有性能度量。 这被称为多类混淆矩阵。 例如,在响应变量中存在3个类X,Y,Z,因此对于每个类的回忆将计算如下:
Recall_X = TP_X /(TP_X + FN_X)
Recall_Y = TP_Y /(TP_Y + FN_Y)
Recall_Z = TP_Z /(TP_Z + FN_Z)
Thuy Pham的答案:
从不同的角度(数据准备或模型构建),有几种方法使模型对离群值更加鲁棒。
离群值通常根据分布来定义。 因此,可以在预处理步骤(在任何学习步骤之前),通过使用标准偏差(对于正常)或四分位范围(对于不正常/未知)作为阈值水平,来去除异常值。
此外,如果数据具有明显的长尾,则数据变换 (例如,对数变换)可能会有帮助。 当与收集仪器的灵敏度相关的异常值可能不能精确记录小值时, Winsorization可能是有用的。 这种类型的变换(以Charles P.Winsor(1895-1951)命名)具有与限幅信号相同的效果(即用极限值替代极值数据值)。 减少异常值影响的另一个选择是使用平均绝对差异而非均方差。
对于模型构建,一些模型抵抗异常值(例如基于树的方法 )或非参数测试。 类似于中值效应,树模型在每个分裂中将每个节点划分为两个。 因此,在每个分裂处,桶中的所有数据点可以被等同地对待,而不管它们可能具有的极值。 这项研究[Pham 2016]提出了一个检测模型,结合数据的四分位数信息来预测数据的异常值。
参考文献:
[Pham 2016] TT Pham,C. Thamrin,PD Robinson和PHW Leong。 强制振荡测量中的呼吸伪影去除:机器学习方法。 IEEE Transactions on Biomedical Engineering,2016。
via KDnuggets,雷锋网编译
雷峰网版权文章,未经授权禁止转载。详情见转载须知。